Classification
Objectives:
The objective of this document is to give a brief introduction to classification methods and model evaluation. After completing this tutorial you will be able to:
- Generate classification models
- Evaluate model performance
Let’s load the data:
data(iris)
head(iris)## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1 5.1 3.5 1.4 0.2 setosa
## 2 4.9 3.0 1.4 0.2 setosa
## 3 4.7 3.2 1.3 0.2 setosa
## 4 4.6 3.1 1.5 0.2 setosa
## 5 5.0 3.6 1.4 0.2 setosa
## 6 5.4 3.9 1.7 0.4 setosashuffleIris <- iris[sample(nrow(iris)),] #Shuffle the dataset
trainIris <- shuffleIris[1:100,] #Subset the training set
testIris <- shuffleIris[101:150,-5] #Subset the test set without the class column
testClass <- shuffleIris[101:150,5] #Get test classes into a separate vectork-Nearest Neighbors Classification
require(class)
predClass <- knn(trainIris[,-5],testIris, trainIris[,5], k = 5) #knn(trainvariables, testvariables, trainclasses, k)
require(caret)
confusionMatrix(testClass, predClass)## Confusion Matrix and Statistics
##
## Reference
## Prediction setosa versicolor virginica
## setosa 15 0 0
## versicolor 0 18 2
## virginica 0 1 14
##
## Overall Statistics
##
## Accuracy : 0.94
## 95% CI : (0.8345, 0.9875)
## No Information Rate : 0.38
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.9094
##
## Mcnemar's Test P-Value : NA
##
## Statistics by Class:
##
## Class: setosa Class: versicolor Class: virginica
## Sensitivity 1.0 0.9474 0.8750
## Specificity 1.0 0.9355 0.9706
## Pos Pred Value 1.0 0.9000 0.9333
## Neg Pred Value 1.0 0.9667 0.9429
## Prevalence 0.3 0.3800 0.3200
## Detection Rate 0.3 0.3600 0.2800
## Detection Prevalence 0.3 0.4000 0.3000
## Balanced Accuracy 1.0 0.9414 0.9228This has a pretty high accuracy. This is partly due to how clean our data is.
The confusion matrix gives us a table that tells the overlap between true class and the predicted class. The columns give us the true class while the rows give us the predicted ones. Take a look at the virginica column in the confusion matrix. One instance of data that is actually virginica is classified as versicolor. Confusion matrix gives us information about the confusion of the classes by the model.
Naive Bayes Classification
require(e1071)
naiveModel <- naiveBayes(Species~., data = trainIris)
predClass <- predict(naiveModel, testIris)
confusionMatrix(testClass, predClass)## Confusion Matrix and Statistics
##
## Reference
## Prediction setosa versicolor virginica
## setosa 15 0 0
## versicolor 0 18 2
## virginica 0 2 13
##
## Overall Statistics
##
## Accuracy : 0.92
## 95% CI : (0.8077, 0.9778)
## No Information Rate : 0.4
## P-Value [Acc > NIR] : 1.565e-14
##
## Kappa : 0.8788
##
## Mcnemar's Test P-Value : NA
##
## Statistics by Class:
##
## Class: setosa Class: versicolor Class: virginica
## Sensitivity 1.0 0.9000 0.8667
## Specificity 1.0 0.9333 0.9429
## Pos Pred Value 1.0 0.9000 0.8667
## Neg Pred Value 1.0 0.9333 0.9429
## Prevalence 0.3 0.4000 0.3000
## Detection Rate 0.3 0.3600 0.2600
## Detection Prevalence 0.3 0.4000 0.3000
## Balanced Accuracy 1.0 0.9167 0.9048This also has a pretty high accuracy.
Decision Trees
require(rpart)
decisionModel <- rpart(Species~., data = trainIris)
predClass <- predict(decisionModel, testIris, type = "class")
confusionMatrix(testClass, predClass)## Confusion Matrix and Statistics
##
## Reference
## Prediction setosa versicolor virginica
## setosa 15 0 0
## versicolor 0 18 2
## virginica 0 3 12
##
## Overall Statistics
##
## Accuracy : 0.9
## 95% CI : (0.7819, 0.9667)
## No Information Rate : 0.42
## P-Value [Acc > NIR] : 1.676e-12
##
## Kappa : 0.848
##
## Mcnemar's Test P-Value : NA
##
## Statistics by Class:
##
## Class: setosa Class: versicolor Class: virginica
## Sensitivity 1.0 0.8571 0.8571
## Specificity 1.0 0.9310 0.9167
## Pos Pred Value 1.0 0.9000 0.8000
## Neg Pred Value 1.0 0.9000 0.9429
## Prevalence 0.3 0.4200 0.2800
## Detection Rate 0.3 0.3600 0.2400
## Detection Prevalence 0.3 0.4000 0.3000
## Balanced Accuracy 1.0 0.8941 0.8869require(rpart.plot)
prp(decisionModel) 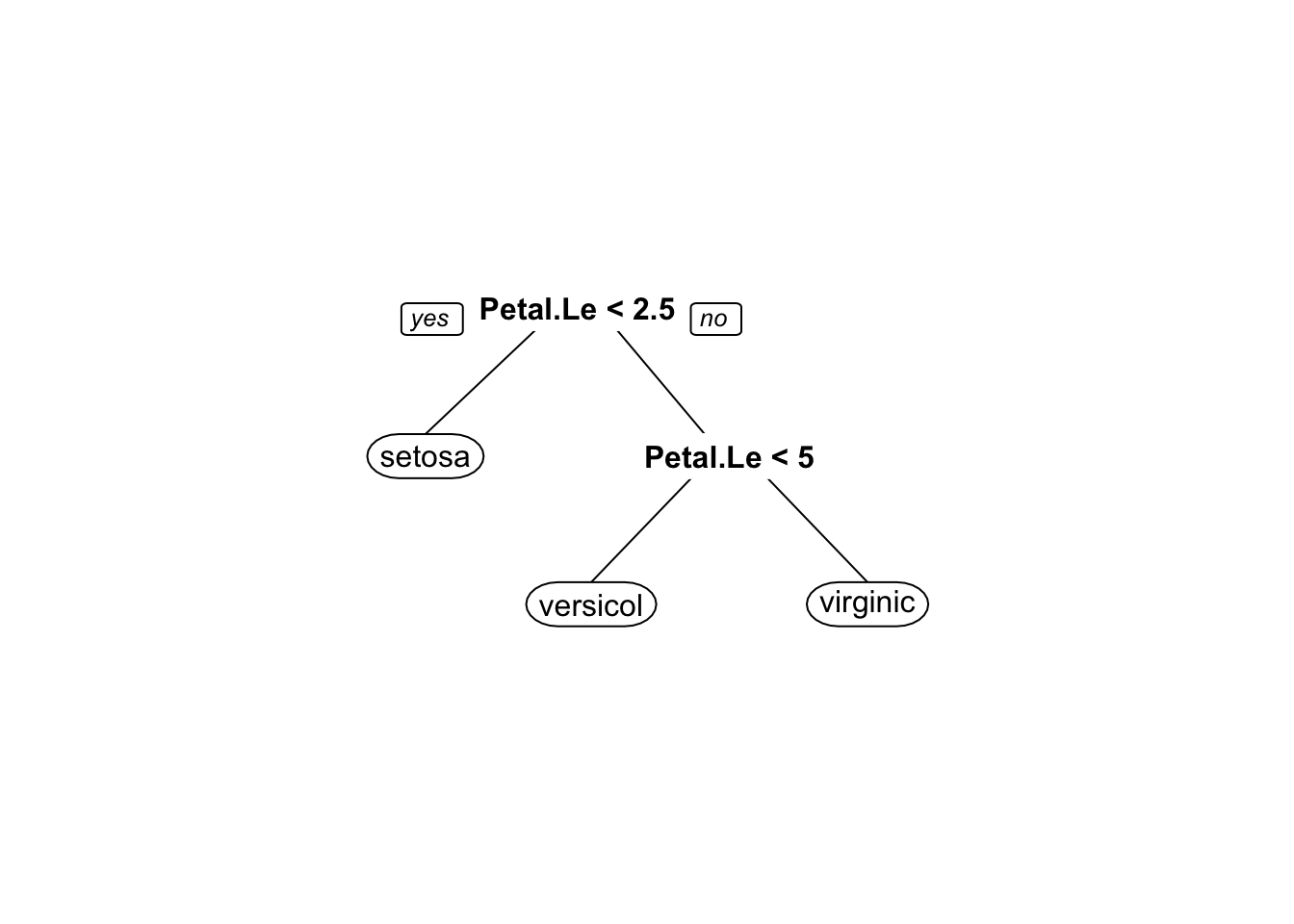
Keep in mind that due to sampling your decision tree can look different than this.
This also has a very high accuracy; however, accuracy in itself is not sufficient in evaluating models. We should also consider the specificity and sensitivity values. Because, if there is an imbalance in the class, say you have 1000 class A in your test data and 10 class B. Then, if you label all the test data as class A, you will have high accuracy (1000/1010), however you weren’t able to detect any instances with class B, so your model is not very good. Sensitivity and Specificity both needs to be high for your model to be good.
Evaluation Measures
There are several evaluation measures reported in the outputs of the models generated above. Three most important values are ‘Sensitivity’, ‘Specificity’ and ‘Accuracy’. Accuracy gives you which percent of the data you correctly classified. However this is not a good measure if there is a class unbalance. For instance, let’s say that you have 100 data points of which 95 are class a and 5 are class b. You can classify all 100 points as class a and you will still have 95% accuracy, even though you failed to find any data that belongs to class b. This is why we need sensitivity and specificity. Sensitivity tells us how many of the data that are of class a, we were able to classify as class a. In this example, this would be 1. Because every data that belonged to class a was classified as class a. Specificity tells us how many data points that were class b were classified as class b. In this example, specificity will be zero because none of the data that were class b was classified as such. Ideally, we want both of these values to be close to one. If all your values are close to one, then you have a good model.
Useful Links
- Caret package documentation: http://www.jstatsoft.org/v28/i05/paper
- This webpage holds examples and advanced methods for generating both classification and regression models using
caretpackage.
- This webpage holds examples and advanced methods for generating both classification and regression models using
- Accurately determining prediction error: http://scott.fortmann-roe.com/docs/MeasuringError.html
- This document explains the details of error measurements
- PCA revisited: using principal components for classification of faces: https://www.r-bloggers.com/pca-revisited-using-principal-components-for-classification-of-faces/
- A tutorial on how you can use PCA to a classification problem. For more details of the PCA, you can refer to our exercise on Dimentionality Reduction